그래프 vs 트리?
| 구분 | 그래프(Graph) | 트리(Tree) |
| 정의 | 객체 혹은 노드(Node)와 그것을 연결하는 간선(Edge)으로 모인 구조 | 그래프의 한 종류이고 방향성이 없으며 순환하지 않음 |
| 방향성 | 무방향 혹은 유방향으로 가능 | 무방향 그래프 |
| 순환성 | 순환 가능 자기 자신을 연결하는 간선(Self-Loop) 가능 순환(Cyclic), 비순환(Acyclic) 모두 가능 | 순환 불가능 자기 자신 연결 간선(Self-Loop) 불가능 비순환 그래프(Acyclic Graph) |
| 루트 | 루트의 개념이 있거나 없을 수 있음 | 하나의 루트 노드 존재 |
| 모델 | 네트워크 모델 | 계층 모델 |
| 순회 | 넓이 우선 탐색(BFS) 깊이 우선 탐색(DFS) | 전위(Pre) / 중위(In) / 후위(Post) 순회 방식 |
| 간선수 | 그래프에 따라 다르며 없을 수도 있음 | N개의 노드(Node)라면 N-1개 |
Tree 트리
: 그래프의 한 종류이고 방향성이 없으며 순환하지 않음.
한 노드가 여러 노드를 가르킬 수 있는 비선형적 자료구조.
트리의 종류
-편향 트리
-이진 트리
-이진 탐색 트리 (BST)
-m원 탐색 트리
-균형 트리
사용 예시
-파일이나 폴더와 같은 계층적 데이터 저장
-효율적인 검색속도가 필요한 경우
-우선순위 큐에서 사용하는 Heap 정렬
-데이터베이스 인덱싱 (B-Tree, B+Tree, AVL-Tree)
-Trie: 사전을 정의하는 데 사용되는 특별한 종류의 트리
Binary Tree 이진 트리
: 각 노드가 최대 2개(0-2)의 자식 노드를 가지는 트리
이진트리 유형
-정 이진 트리(full binary tree) (or 엄격한 (strict) 이진 트리)
: 모든 노드가 두 개의 자식 노드를 가지는 트리
-포화 이진 트리(Perfect Binary tree)
: 모든 노드가 두 개의 자식 노드를 가지고, leaf 노드(terminal node)가 모두 같은 레벨인 트리

높이가 h일 때 노드 갯수는 2k+1 - 1 개를 가진다는 특징이 있음.
Leaf 노드의 갯수는 2h 개
-완전 이진 트리(Complete Binary Tree)
조건1 : 마지막 레벨을 제외하고 모든 노드가 채워진 트리 구조
조건2 : 노드는 왼쪽에서 오른쪽으로 채워져야 함
-> 위 조건을 모두 만족하면 완전 이진 트리
1차원 배열로 표현하는 이진 트리

- 왼쪽 트리는 루트 노드부터 level 순, 그리고 왼쪽에서 오른쪽 순서로 각 노드에 index를 붙여 표현.
- 따라서 완전 이진 트리는 위의 그림과 같이 배열을 빈틈없이 모두 채울 수 있음.

- 왼쪽 노드에서 오른쪽 노드 순서로 채워지기 때문에 경사 이진 트리같은 경우 불필요한 공간이 낭비 될 수 있고,
배열 크기 이상 노드를 추가할 수 없다는 단점이 있음
- 중간이 비어있는 트리의 경우(왼쪽 자식 노드는 있는데 오른쪽 자식 노드는 없는 경우) 배열 사이에 null 값이 들어간 구조로 표현
- 0번 index는 비우고 1번 index 부터 Root Node를 채움 -> 탐색을 쉽게 할 수 있게 해줌
i) 루트 노드의 인덱스가 0인 경우
| 루트 노드 | 1 |
| 노드 i의 부모 | i/2 |
| 노드 i의 왼쪽 자식 | i * 2 |
| 노드 i의 오른쪽 자식 | i * 2 + 1 |
ii) 루트 노드의 인덱스가 1인 경우
| 루트 노드 | 0 |
| 노드 i의 부모 | (i - 1) / 2 |
| 노드 i의 왼쪽 자식 | i*2 + 1 |
| 노드 i의 오른쪽 자식 | i*2 + 2 |
e.g. 6의 인덱스 구하기

6은 노드 3의 왼쪽 자식 => i * 2 = 3 * 2 = 6
∴ 6의 인덱스 = 6
- 연결 리스트를 사용하여 이진트리를 구성하는 경우
:배열 보다는 접근 속도는 느리지만(인덱스를 통한 random access가 불가하기 때문)
삽입, 삭제가 쉽고 노드를 포인터로 연결하는 개념이기 때문에 노드 수에 제한이 없음
Tree Traversal 트리 순회 알고리즘
: 트리 순회란 트리 구조에서 각 노드를 한 번씩 방문하는 과정.
노드 방문을 어떤 순서로 하느냐에 따라 세 가지로 구분.
1. 전위 탐색 (preorder)
: 깊이 우선 순회(DFT, Depth-First Traversal) 라고도 함
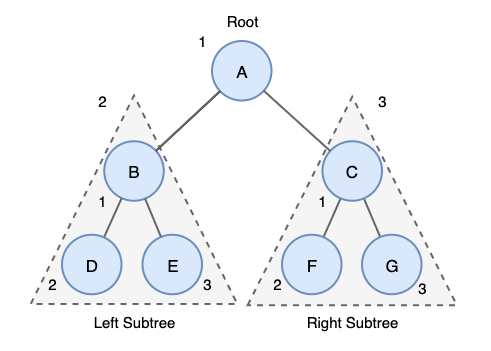
- 루트 노드를 가장 먼저 방문
- 이후 왼쪽 서브 트리를 전위 순회 (재귀 호출)
- 오른쪽 서브 트리를 전위 순회 (재귀 호출)
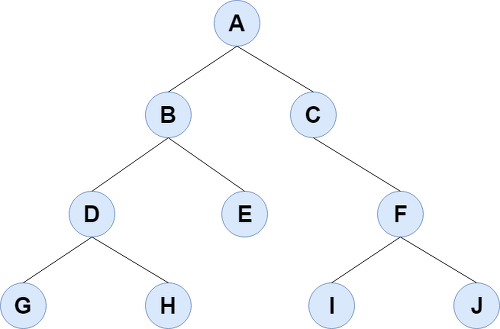
현재 노드를 가장 먼저 방문
->왼쪽 자식과 오른쪽 자식을 현재 자식보다 나중에 방문
위 그래프를 전위순회로 방문하게 된다면
A -> B -> D -> G -> H -> E -> C ->F ->I -> J
순서로 방문하게 됨
2. 중위 탐색 (inorder)
: 왼쪽 오른쪽 대칭 순서로 순회를 하기때문에 대칭 순회(symmetric traversal)라고도 함
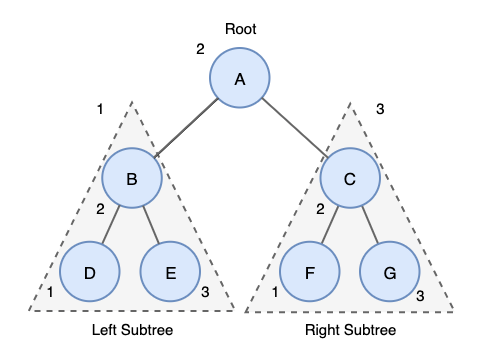
- 먼저 왼쪽 서브 트리를 중위 순회
- 그 다음 중간에 루트 노드를 방문
- 오른쪽 서브 트리를 중위 순회

우선 왼쪽 자식을 방문하고, 현재 노드를 방문
그 다음 오른쪽 자식 노드를 방문
-> 현재 노드를 중간에 방문한다고 해서 중위순회
G -> D -> H -> B -> E -> A -> C ->I -> F -> J
순서로 방문하게 됨
3. 후위 탐색 (postorder)
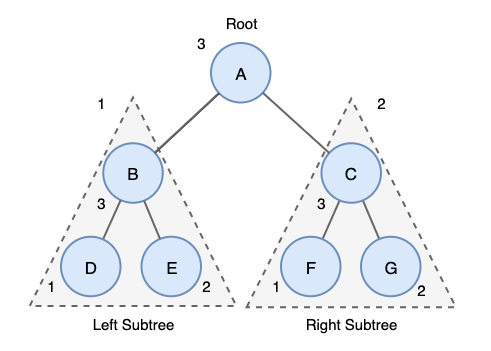
- 먼저 왼쪽 서브 트리를 후위 순회
- 오른쪽 서브 트리를 후위 순회
- 루트 노드를 가장 마지막에 방문

왼쪽 자식, 오른쪽 자식 노드를 우선적으로 방문
-> 현재 노드를 가장 나중에 방문
G -> H -> D -> E -> B ->I -> J -> F -> C -> A
순서로 방문하게 됨
-출처
https://cdragon.tistory.com/21
https://cdragon.tistory.com/19
'Web Development > Data Structure 자료구조' 카테고리의 다른 글
| [자료구조] Priority Queue 우선순위 큐, Heap 힙 (1) | 2023.11.27 |
|---|---|
| [자료구조] Binary Search Tree 이진탐색트리 (1) | 2023.11.24 |
| [자료구조] Deque 덱 (0) | 2023.11.24 |
| [자료구조] Graph 그래프 (0) | 2023.11.24 |
| [자료구조] Queue 큐 (1) | 2023.11.23 |

