Binary Search Tree 이진탐색트리
트리 구조 자체적으로는 트리 노드를 하나하나씩 방문하여 탐색해야 하기 때문에 시간 복잡도 측면에서 큰 이점이 없음.
-> 더 빠른 탐색을 위해서 Binary Search와 마찬가지로 O(log₂n)의 시간 복잡도를 가지도록 고안됨 (데이터의 특성에 제약을 줌)
이진탐색트리의 특성
- 노드의 왼쪽 서브 트리에는 루트 노드보다 작은 값이 들어있다.
- 노드의 오른쪽 서브 트리에는 루트 노드보다 큰 값이 들어있다.
- 서브 트리 또한 이진 탐색 트리 구조이다.
- 중복된 값은 일체 없다.

- 루트 노드인 5를 기준으로 왼쪽 서브 트리에는 5보다 작은 수로 구성 되어있고 오른쪽 서브 트리에는 5보다 큰 수로 구성됨

- 하위의 서브 트리에서도 각 루트 노드를 기준으로 왼쪽과 오른쪽이 각각 작은 수와 큰 수로 나뉘어져 있음
트리의 최솟값

트리 구조의 가장 왼쪽 끝에 위치한 노드
만약 1의 왼쪽 자식 노드가 있다면 그 값이 최솟값
트리의 최댓값

트리 구조의 가장 오른쪽 끝에 위치한 노드
만약 9의 오른쪽 자식 노드가 있다면 그 값이 최댓
- 이진 탐색 트리는 중위 탐색을 하면 오름 차순으로 숫자를 가져올 수 있음
이진탐색트리의 연산
1. 생성
이진 탐색 트리를 생성할 때는 데이터의 크기를 비교해 가면서 노드를 추가함
[50, 15, 62, 80, 7, 54, 11]
위의 데이터들로 이진 탐색 트리를 생성해 볼 때
- 50이 배열의 첫 번째 데이터이기 때문에 루트 노드로 트리에 삽입
- 다음 요소를 계속해서 읽고 해당 노드가 루트 노드 요소보다 작으면 왼쪽 하위 트리의 루트로 삽입
- 그렇지 않으면 오른쪽 하위 트리의 오른쪽 루트로 삽입

2. 삽입
삽입 과정의 특징
- 가장 먼저 해당 데이터가 자신이 들어갈 위치를 찾아야 함
- 중복된 데이터는 삽입하지 않음
-> 숫자를 삽입하려 할 때 탐색 과정에서 같은 숫자가 있는 것을 발견하면 삽입하지 않고 그대로 종료해야 함
- 데이터를 삽입하거나 삭제하더라도 그 특성이 유지되어야 함
- 추가된 노드는 트리의 leaf 노드에 삽입
(이진트리의 특성 상 자식 노드가 3개 이상이면 안되기 때문)
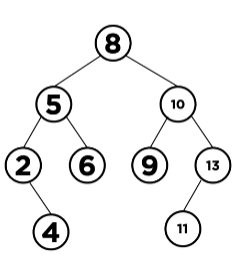
만약, 1이라는 데이터를 위 이진 탐색 트리에 삽입하고자 한다면,
- 먼저 루트 노드인 8과 비교
- 1은 루트노드 8보다 더 더 작기 때문에 왼쪽 노드인 5와 다시 비교
- 5와 비교했을 때도 더 작기 때문에 또 왼쪽 노드로 이동하여 2와 비교
- 2와 비교했을 때도 더 작고, 2의 왼쪽 자식 노드가 비어있기 때문에 2의 왼쪽 노드에 삽입
3. 삭제
데이터의 삭제는 leaf 노드만 삭제가 가능한 것이 아니라 트리 구조 중간에 위치한 노드도 삭제 될 수 있기 때문에 더 까다로움
삭제를 위해서는 우선 삭제할 노드의 위치를 찾아야 함
삭제할 노드 위치의 경우의 수
i) 삭제할 데이터가 leaf인 경우
ii) 한 개의 자식 노드를 가질 경우
iii) 두 개의 자식 노드를 가질 경우
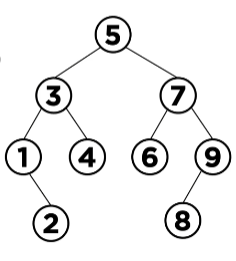
위와 같은 이진탐색트리를 예로 들어 생각했을 때
i) 삭제할 데이터가 leaf인 경우
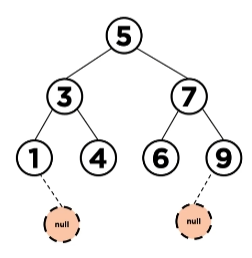
삭제 할 데이터가 leaf인 경우는 초기 그림 상에서 2와 8을 의미함
-> null을 부모 노드에게 리턴시켜서 자신을 가리키던 자식 포인터를 null로 바꿔주면 됨
ii) 한 개의 자식 노드를 가질 경우
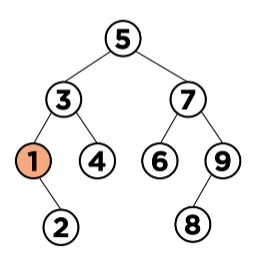
삭제하고자 하는 노드가 한 개의 자식 노드를 가질 경우에
-> 해당 노드의 자식 노드를 1의 부모 노드였던 3 자식 노드를 가리키던 포인터와 연결시켜 주면 됨
그러면 다음 그림과 같이 되어 이진 탐색 트리의 속성이 유지됨
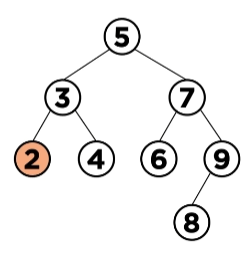
iii) 두 개의 자식 노드를 가질 경우
삭제 하고자 하는 노드가 두 개의 자식 노드를 가질 경우에는 두 가지 옵션이 존재함
- 왼쪽 서브 트리의 최댓값과 교체
- 오른쪽 서브 트리의 최솟값과 교체
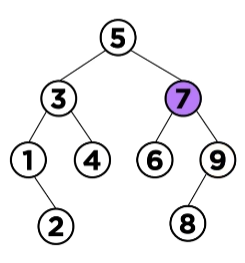
오른쪽 서브트리의 최솟값과 교체하는 방법을 사용하는 예시
오른쪽 서브트리의 최솟값 즉, inorder 순회의 다음 노드는 successor라고 함.
과정
- 삭제할 노드를 찾는다.
- 삭제할 노드의 successor 노드를 찾는다.
- 삭제할 노드와 successor 노드의 값을 바꾼다.
- successor 노드를 삭제한다. (연결을 끊는다.)
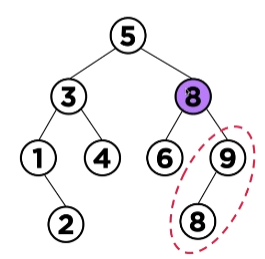
7의 오른쪽 서브 트리에는 8과 9가 존재함
-> 이 중 최솟값인 8(successor 노드)과 삭제하고자 하는 노드 7을 교체
이런 과정을 통해 8이라는 데이터가 중복되기 때문에 leaf 노드의 8을 지워주어야 함
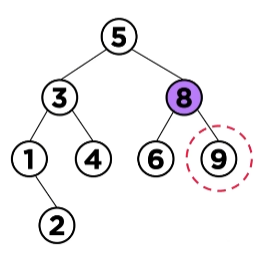
이때 지워야 하는 8은 leaf 노드이기 때문에 null을 대입하여 삭제
Binary Search Tree의 시간복잡도
| Access | Search | Insertion | Deletion | |
| 평균 | O(log₂n) | O(log₂n) | O(log₂n) | O(log₂n) |
| 최악의 경우 | O(log₂n) | O(log₂n) | O(log₂n) | O(log₂n) |
-출처
'Web Development > Data Structure 자료구조' 카테고리의 다른 글
| [자료구조] Priority Queue 우선순위 큐, Heap 힙 (1) | 2023.11.27 |
|---|---|
| [자료구조] Tree 트리 (0) | 2023.11.24 |
| [자료구조] Deque 덱 (0) | 2023.11.24 |
| [자료구조] Graph 그래프 (0) | 2023.11.24 |
| [자료구조] Queue 큐 (1) | 2023.11.23 |

